接着上一篇 TLS Perfect Forward Secrecy 之 RSA 缺陷 继续来看看 DH/ECDHE 如何解决这个问题。

前面提到 RSA 做密钥协商过程中，最关键的缺陷是客户端用公钥加密了 PreMaster Key，服务器用私钥解密 PreMaster Key。理想中更好的方法是 公钥/私钥只用来对证书签名，不参与到密钥协商的过程中来，换句话说，希望通信的双方能独立计算出对称加密的密钥。于是密码学家找到了尘封已久的，几乎与 RSA 同时出现的 DH 算法。

其实我一直有一个疑问：既然问题出在传送 PreMaster Key，那么客户端不发送 PreMaster Key 不就行了？握手的过程中已经有了 2 个随机数了，难道一定要 3 个随机数才能生成 master key 吗？

首先来看一下 DH 算法的数学基础。

+-------------------------------------------------------------------+
|                    Global Pulic Elements                          |
|                                                                   |
|       p                               prime number                |
|       a                               prime number, a < p         |
+-------------------------------------------------------------------+
+-------------------------------------------------------------------+
|                    User A Key Generation                          |
|                                                                   |
|       Select private Xa               Xa < p                      |
|       Calculate public Ya             Ya = a^Xa mod p             |
+-------------------------------------------------------------------+
+-------------------------------------------------------------------+
|                    User B Key Generation                          |
|                                                                   |
|       Select private Xb               Xb < p                      |
|       Calculate public Yb             Yb = a^Xb mod p             |
+-------------------------------------------------------------------+
+-------------------------------------------------------------------+
|               Calculation of Secret Key by User A                 |
|                                                                   |
|       Secret Key K                    K = Yb^Xa mod p             |
+-------------------------------------------------------------------+
+-------------------------------------------------------------------+
|               Calculation of Secret Key by User B                 |
|                                                                   |
|       Secret Key K                    K = Ya^Xb mod p             |
+-------------------------------------------------------------------+

上面一共出现了 a, p, Xa, Ya, Xb, Yb, K 共 7 个数，其中：

  • 公开的数：a, p, Ya, Yb
  • 非公开数：Xa, Xb, K

通常情况下，a 一般为 2 或 5，而 p, Xa 和 Xb 的取值也非常大，其复杂度至少为 O(p^0.5)。对于攻击者来说，已知 Ya，Xa 的求解非常困难，同理 Xb 的求解也很困难，所以攻击者难以求出 K，所以 DH 能够保证通信双方在透明的信道中安全的交换密钥。

看完了理论基础，我们用通俗的语言比较下 DH 和 RSA：

  • DH 是用来协商创造密钥的，DH 不能直接用来对数据进行加密解密。
  • RSA 可以用来加密解密，也可以用来传递密钥（尽管本文开头说了传递密钥有安全隐患）
  • 注意：DH 是协商创造密钥，而 RSA 是传递信息。

RSA算法的流程

  • 客户端对服务器发起请求，服务器首先回复自己的公钥（公钥明文传输）
  • 客户端使用随机数算法，生成一个密钥 S，使用收到的公钥进行 加密，生成C，把C发送到服务器
  • 服务器收到 C，使用公钥对应的私钥进行解密，得到 S。

上述的 S 就是开头提到的 Premaster Key。

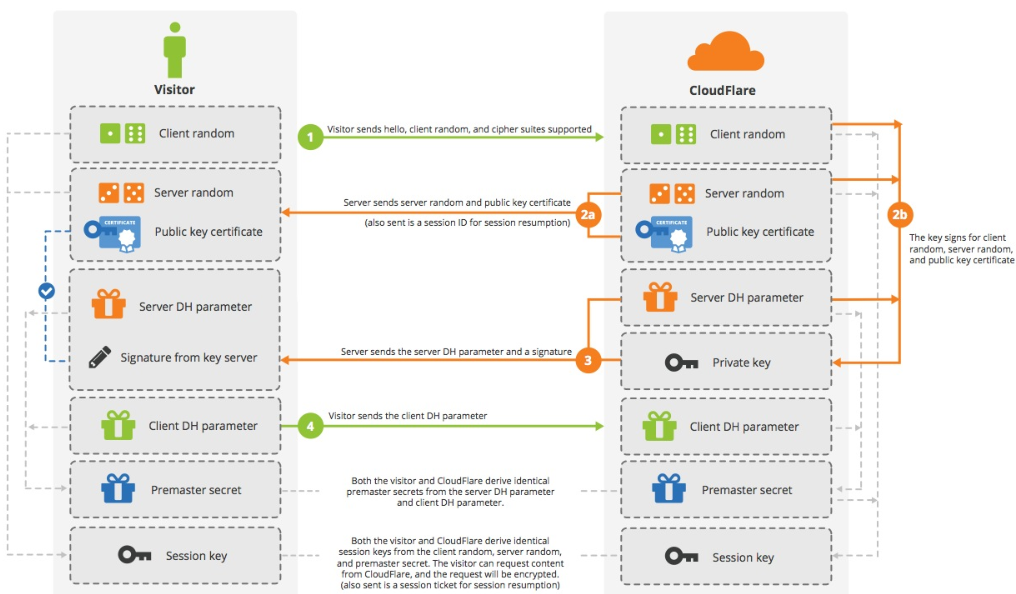
DH协商的流程

  • 客户端计算一个随机值 Xa，使用 Xa 作为指数，即计算 Pa = q^Xa mod p，其中q和p是一对值。客户端把 Pa 发送至服务器，Xa 作为自己私钥。
  • 服务器流程一样，生成一个随机值 Xb，使用 Xb 作为指数，计算 Pb = q^Xb mod p，将结果 Pb 发送至客户端，Xb自己保存。
  • 客户端收到 P b后计算 Sa = Pb ^Xa mod p；服务器收到Pa后计算Sb = Pa^Xb mod p
  • 算法保证了 Sa = Sb = S，密钥协商成功，S为 Premaster Key.

不难看出，上面的过程中服务器私钥没有参与进来，也就是说私钥即使泄漏，也不会导致会话加密密钥S被第三方解密，解决了本文开头提到的缺陷。

实际中，服务器私钥只用来身份认证。 更加详细的 DH 算法，请看参考资料1

ECDHE 算法

只要理解DHE密钥交换原理，那么理解ECDHE密钥交换并不难。ECDHE的运算是把DHE中模幂运算替换成了点乘运算，速度更快，可逆更难。

  • 客户端随机生成随机值Ra，计算Pa(x, y) = Ra x Q(x, y)，Q(x, y)为全世界公认的某个椭圆曲线算法的基点。将Pa(x, y)发送至服务器。
  • 服务器随机生成随机值Rb，计算Pb(x,y) - Rb x Q(x, y)。将Pb(x, y)发送至客户端。
  • 客户端计算Sa(x, y) = Ra x Pb(x, y)；服务器计算Sb(x, y) = Rb x Pa(x, y)
  • 算法保证了Sa = Sb = S，提取其中的S的x向量作为 Premaster Key。

下面重点比较一下这些缩写的区别，非常容易混淆….

ECDHE 与 ECDH

字面少了一个E，E代表了 临时，即在握手流程中，作为服务器端，ECDH少了一步计算Pb的过程，Pb用证书中的公钥代替，而证书对应的私钥就是Xb。由此可见，使用ECDH密钥交换算法，服务器必须采用ECC证书；服务器不发送server key exchange报文，因为发送certificate报文时，证书本身就包含了Rb信息。

所以，有 E 的算法都支持 PFS，例如 DHE，ECDHE。

ECDHE 与 RSA

ECDHE（DHE）算法属于DH类密钥交换算法，私钥不参与密钥的协商，故即使私钥泄漏，客户端和服务器之间加密的报文都无法被解密，这叫 Perfect Forward Secrecy。由于ECDHE每条会话都重新计算一个密钥（Ra、Rb），故一条会话被解密后，其他会话仍旧安全。

ECDH 和 ECDSA

EC是椭圆曲线 elliptic curves 的意思，ECDSA 是签名算法，是DSA算法的一个变体。

ECDH 算法服务器端的私钥是固定的，即证书的私钥作为Rb，故 ECDH 不是前向安全，因为私钥泄漏相当于 Rb 泄漏，导致会话密钥可被第三方计算。

具体的算法流程，请参阅这一篇

RSA handshake

参考资料