- Table {:toc}
问题
有一个数组 31,-41,59,26,-53,58,97,-93,-23,84 。现在要求出它的连续子串的最大值。 比如,31,-41,59,26是它的一个连续的子串,他们的和为75。但是75并不是最大值,有一个子串 59,26,-53,58,97它们的和187才是最大的。
解答
《Programming Pearls》第77页开始一共给出了4种解法,前两种非常简单,是大多数人思考几分钟就能想出的方法,但是复杂度却很高,分别为O(n^3)和O(n^2)。后两种解法则非常巧妙,更神奇的是第四种方法居然只有线性复杂度O(n)
解法1、解法2略。
解法 3:分治法
复杂度为O(nlogn)。 分治法在结构上是递归的,在保证不改变原问题的条件下,将问题的规模减小,生成多个子问题,并多次递归调用自身来解决子问题,之后再将子问题的求解结果合并成原问题的解。

对于case1,我们只要比较 ma 和 mb 的大小就可以得出原数组的最大子串的和了。
对于case2, 只要把ma和mb相加即可。以上只是将问题一次分解的过程,我们还需要将问题再分解直到不能在分解或是能直接得出结果为止。
什么时候能直接得出结果?当子数组只有一个元素的时候,此时ma就是它本身(为负数时我们让它为0)。
因此,原数组的最大和 = 2个子数组中最大和的较大者,或者,包括中间分界线的一段连续区域的和。
即,maxsum(orignial)=max(mc,maxsum(a),maxsum(b))
递归结束的条件是,子数组只有一个元素,如果是正返回它本身,为负返回0
代码如下。
int maxSubArray(std::vector<int>& nums) {
return maxsum(nums, 0, nums.size()-1);
}
int maxsum(std::vector<int> &nums, int left, int right) {
if (left > right) {
return 0;
}
if (left == right) {
return nums[left];
}
int mid = (left + right)/2;
int left_max = INT_MIN, right_max = INT_MIN;
int tmp_max = 0;
for (int i = mid; i >= left; i--) {
tmp_max += nums[i];
left_max = std::max(left_max, tmp_max);
}
tmp_max = 0;
for (int i = mid+1; i <= right; i++) {
tmp_max += nums[i];
right_max = std::max(right_max, tmp_max);
}
return std::max(left_max+right_max,
std::max(maxsum(nums, left, mid),
maxsum(nums, mid+1, right)));
}
解法4:扫描法
一次扫描数组即可得出答案,复杂度O(n)。这种方法用文字描述不容易说清楚,下面用每一步运算的图示来表达。伪代码如下:
maxsofar=end=0;
for i=[0,n)
end=max(end+x[i],0)
maxsofar=max(maxsofar,end)

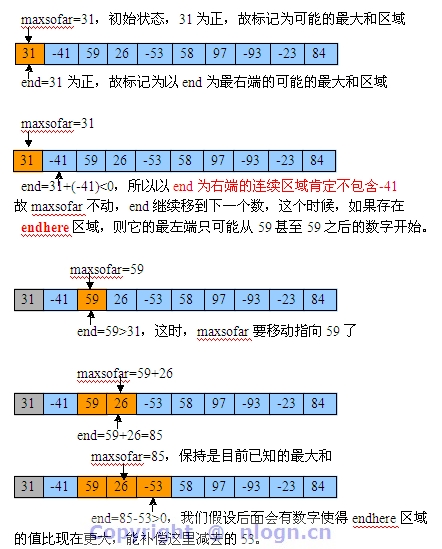
即使后面没有这样的值了,maxsofar中还保存了原来的最大和,有恃无恐。
这里的一条重要原则是目前end 的值必须 >0,如果<0,则不用考虑,立刻放弃end目前的值,将它置为0,并且把end的指针指向58。
以此类推下去,最后可得正确的结果。
总的说来,解法4虽然原理很简单,还是自己很难想出来,甚至看了书上的讲解后还是存有疑惑,等到再读第2遍、第3遍以后,回过头来重新写读书笔记,也许有更多感悟。