在理解一致性 hash 之前，先来看看这个问题是怎么产生的。例如我们有一个数据库，里面存了成千上万张图片，用户访问图片会呈现一定的规律性，比如某段时间内一张照片火了，那么短时间内会有大量的请求访问这张图片，会对数据库造成压力，这时候我们就想到要加一层缓存，这也是系统架构的终极法宝。

所以，这种场景下典型的系统架构如下图所示：

arch

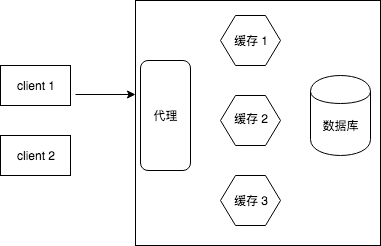
客户端要访问文件名为 A 的图片，代理服务器根据文件名去缓存服务器中查询，如果cache中没有，那么最终去数据库取，同时也把取到的图片文件缓存在某个缓存服务器中。这里有个题外话，通常我们会把文件名 A 通过 hash 函数转换成一段数字，便于操作，这里的 hash 函数与本文的一致性 hash 是不一样的。

那么问题来了：如何将图片均匀的缓存在缓存服务器上呢？

最简单的方式，以文件名为 key，缓存服务器个数为 N，取模得到余数，即 key % N = i，i 是几，就把图片缓存到对应编号的服务器上。

这种方式确实能够将数据 均匀的 分布在缓存上，但是最大的缺点是一旦 N 的数量发生变化，那么几乎所有的 i 都会改变，导致缓存失效。

例如，

key = 5 的文件，在 N = 3 时，缓存在编号为 2 的缓存服务器上。
增加一台服务器，N = 4，那么 key = 5 的文件应该在 1 号服务器上，但事实上它在 2 号。

导致这种情况的根本原因是什么呢？ 我们想让数据均匀分布，但是均匀的算法却依赖于 N ，而 N 直接依赖于服务器的数量！

一致性 Hash 的原理

消除依赖

所以解决的办法就是，让均匀分布的计算方法不依赖于 Redis 的个数 N。

如何实现这一目标呢？

假设我们有一个环形 hash 表，先把 Redis 的某个 metadata（比如 ip 地址），散列到这个 hash 环上。
对每个数据，我们也用某种 hash 算法散列到这个 hash 环上。
结果如下图所示。
一个数据 A 按照顺时针的方式，放到离它最近的一个 redis 上。（比如 bob 放到 S2 上）

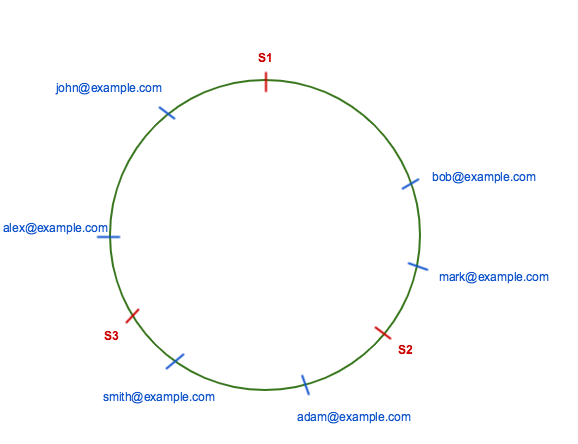
这样，就让一个数据应该存在哪个 redis 上不依赖于 redis 的个数了。

假设现在我们增加了一个 redis S4，如图：

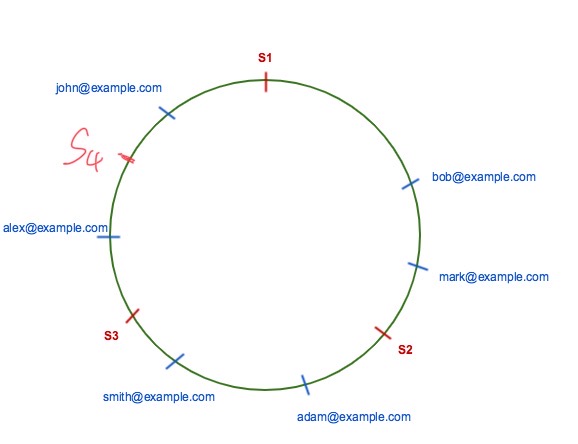
那么，本来应该存在 S1 上的数据 alex@example.com 现在应该在 S4 上，而其他所有的数据都保持不变。

所以，一致性 Hash（环形 hash 法）极大的减少了(注意，不是消除)缓存失效的问题。

引入虚拟节点，优化均衡

接下来进一步优化一个问题：如何避免某个 Redis 存了绝大多数数据导致的不均衡问题？

通过上面的 Hash 环基本原理，我们不难发现：如果环上的节点越多，数据就会分布的越均匀，而实际上我们的 Redis 个数是有限的。

因此，引入了一个 “虚拟节点” 的概念，通过某种机制（比如用不同算法生成每个 redis 节点的位置），让一个物理 redis 在环上有多个虚拟节点。

综上所述，“消除依赖” 和 “虚拟节点” 就是一致性 hash 的基本思想。

上面的算法思想也是最基本的一种，人称环形分割法 Web caching with consistent hashing.

后续有人又提出了各种消除依赖的算法，比如

集合哈希法A Name-Base Mapping Scheme for Rendezvous
跳转哈希法 A Fast, Minimal Memory, Consistent Hash Algorithm
有界载荷一致性哈希 Consistent Hashing and Random Trees:Distributed Caching Protocols for Relieving Hot Spots on the www
悬浮哈希法 Maglev: A Fast and Reliable Software Network Load Balancer

详见参考资料。

具体实现

https://github.com/golang/groupcache 中给了一个具体的实现，总共也就不到 100 行代码，下面来看一下每个函数。

结构体定义

type Map struct {
	hash     Hash
	replicas int
	keys     []int // Sorted 
	hashMap  map[int]string
}

func New(replicas int, fn Hash) *Map {
	m := &Map{
		replicas: replicas,
		hash:     fn,
		hashMap:  make(map[int]string),
	}
	if m.hash == nil {
		m.hash = crc32.ChecksumIEEE
	}
	return m
}

其中：

hash 指的是具体的 hash 函数。
replicas，指的是每个物理节点的虚拟节点的个数。
key，这里的 key 其实就是虚拟节点在环上的值，默认是一个 2^32 整数的环。
hashMap，每个虚拟节点的 hash 位置，对应的物理节点的名字（也可以是 IP）

Add 函数

比如，给定一个 Redis 实例，IP 是 192.168.3.2，我们要把它加到 hash 环上，那么就调用 Add 函数。


// Add adds some keys to the hash.
func (m *Map) Add(keys ...string) {
	for _, key := range keys {
		for i := 0; i < m.replicas; i++ {
			hash := int(m.hash([]byte(strconv.Itoa(i) + key)))
			m.keys = append(m.keys, hash)
			m.hashMap[hash] = key
		}
	}
	sort.Ints(m.keys)
}

假设我们把 IP 192.168.3.2 作为参数传入，replicas 为 3，那么 Add 会计算出 3 个位置。

m.keys 其实可以看成是 hash 环，存了这 3 个位置。
m.hashMap 是我们可以从 hash 位置反推出 Redis 的 IP 192.168.3.2。注意，最后一定要排序 sort。

注意：这里的数组 keys 其实才是真正逻辑上的 “环”， hashMap 只是起到了保存原始 key string 的作用。

arch

上面的代码算出 hash 以后，把它加入到 m.keys 的 “环” 上，最后 sort 从小到大排序。

Get 函数

Add 函数是针对 Redis 节点的，它把 Redis 放到 hash 环上合适的位置。 Get 函数就是针对数据的了。

func (m *Map) Get(key string) string {
	if m.IsEmpty() {
		return ""
	}

	hash := int(m.hash([]byte(key)))

	// Binary search for appropriate replica.
	idx := sort.Search(len(m.keys), func(i int) bool { return m.keys[i] >= hash })

	// Means we have cycled back to the first replica.
	if idx == len(m.keys) {
		idx = 0
	}

	return m.hashMap[m.keys[idx]]
}

假设我们有一个数据 data 作为 Get 的参数传入，

通过 sort.Search 找出应该放到 hash 环上的那个 Redis 虚拟节点上。
通过 m.hashMap[m.keys[idx]] 获得 Redis 的具体 IP 192.168.3.2。
然后 client 就去这个 IP 的 Redis 上读取缓存了。

一致性 Hash 的原理#

消除依赖#

引入虚拟节点，优化均衡#

具体实现#

结构体定义#

Add 函数#

Get 函数#

参考资料#