如何存储和表示 B+ 树
前面已经知道,page 是代表 B+ 树被序列化到了磁盘上的结构,一个 page 就是一个 B+ 树节点,通过 mmap 把磁盘上的页映射到内存,然后用 unsafe.Pointer(p) 直接把二进制序列化成 page 结构。也正因为如此,x86 架构上生成的 db 文件是不能在 ARM 架构的机器上打开的。
而 node 结构同样也表示内存中一个 B+ 树的节点,node 与 page 的区别是 node 按需创建的,对于不需要修改的B+树节点,boltdb直接从page中读取数据,当需要修改某个 B+ 树节点时,比如插入删除数据,boltdb 从 page 结构生成成 node 。(此处存疑,我觉得应该是 Cursor 在游走的过程中就会把 page 转化成 node)
Bucket.node() 函数中就有如下一段话
func (b *Bucket) node(pgid pgid, parent *node) *node {
// Retrieve node if it's already been created.
if n := b.nodes[pgid]; n != nil {
return n
}
// Read the page into the node and cache it.
n.read(p)
b.nodes[pgid] = n
}
换句话说,boltdb 不会修改而是只读 mmap 映射的内存,当需要修改时,在内存中另外开辟内存并构造 node 结构,这个新分配的内存属于进程的 heap memory。
需要注意的是,当读取page构建node时,inode的key与value是直接引用的page的地址,即node构建后并非完全不在依赖其page中的数据。但是随着数据库增大,当boltdb需要重新mmap以扩展存储空间时,boltdb需要执行dereference操作。下面的图来自参考资料 1
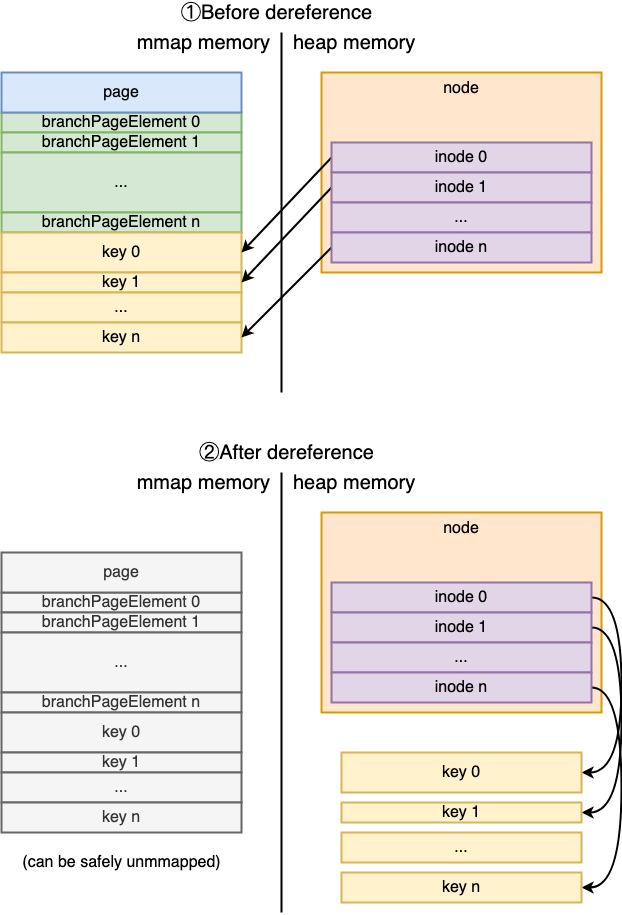
总结
一个 db 文件,它被划分成了 n 多个 page 页面,每一个 page 页面除了开头几个元数据以外,存储的是 B+ 树的中间节点或者是叶子节点信息。
在逻辑上,这些 page 组成了一棵 B+ 树,但是与课本上看到的节点之间用指针指向不同,这里没有指针,只有 page id,所有节点之间的跳转都是用 page id 计算出这个 page 在 db 文件的哪个位置,然后直接加载二进制进入 page 结构体。
比如 分支节点 branchPageElement
type branchPageElement struct {
pos uint32
ksize uint32
pgid pgid // 子节点的页面ID
}
假如在某个查询过程中,现在 cursor 到了某个分支节点,通过比较 key 的大小,锁定了这一个 branchPageElement,接下来要去它的子节点了,怎么去呢? 通过 pgid 获取子节点。
B+ 树的插入和删除
插入和删除的代码非常简单,就是修改 叶子节点的 inodes 数组,把新的数据插入,或者把数据删除。
func (n *node) put(oldKey, newKey, value []byte, pgid pgid, flags uint32) {
// Find insertion index.
index := sort.Search(len(n.inodes), func(i int) bool {
return bytes.Compare(n.inodes[i].key, oldKey) != -1 })
inode := &n.inodes[index]
inode.flags = flags
inode.key = newKey
inode.value = value
inode.pgid = pgid
}
// del removes a key from the node.
func (n *node) del(key []byte) {
// Find index of key.
index := sort.Search(len(n.inodes), func(i int) bool {
return bytes.Compare(n.inodes[i].key, key) != -1 })
// Delete inode from the node.
n.inodes = append(n.inodes[:index], n.inodes[index+1:]...)
// Mark the node as needing rebalancing.
n.unbalanced = true // 只要有元素删除,就标记 unbalanced
}
但是,如果你刚刚复习了 B+ 树的原理,肯定会说插入删除会破坏 B+ 树的性质,需要做出各种调整。没错,boltdb 把这些操作延迟到了在事务 commit 的时候,等到要把 B+ 树写入到文件时才调整结构。
B+ 树的分裂和平衡
首先思考一个问题:假设之前修改了 B+ 树(有可能增加key,也有可能是删除key),并且没有在做完 put、del 操作后立刻调整树的结构,那么现在该如何开始呢?
这也是之前困扰我的地方,书上教的方法都是对叶子节点做完操作后,立刻开始调整树结构,并且有各种判断条件,非常负载。
这是典型的理论学习与工程实践有很大区别的地方。一个真正的数据库引擎,比如 boltdb,需要支持并发的读写,要支持事务,MVCC,有很多东西需要考虑,并且还要让代码尽可能的简单。
boltdb 调整 B+ 树结构依靠rebalance()和spill() 两个函数。
rebalance用于检查node是否由于删除了inode而导致数据填充率低于阈值,并将数据填充率低于阈值的node与其兄弟节点合并,rebalance还会将只有一个孩子的根节点与该其唯一的孩子合并。spill则可以进一步分为两个步骤,spill首先会检查并将填充率过高的节点拆分为多个小节点(split),并维护B+Tree的结构,然后将更新后的节点写到新的page中。
因此,在事务提交时,boltdb会先对B+Tree执行rebalance操作再执行spill操作。
通过以上的讲解可以看出 boltdb 调整树结构是从一个宏观的角度进行的:
- 假设给我一个 B+ 树,已知它不满足平衡条件需要调整。
- 第一步,自底向上,把所有能合并的节点都合并了。
- 第二步,自底向上,把所有需要分裂的节点都分裂成一个或者多个。
相比学习 B+ 树原理时,每次操作叶完子结点后各种操作晕头转向,这样的方式简洁了很多。
// 数据先写入 inodes -> rebalance() - > spill() -> freelist()
// -> 写入B+树到磁盘 -> 写入 meta data
func (tx *Tx) Commit() error {
// Rebalance nodes which have had deletions.
tx.root.rebalance()
// spill data onto dirty pages.
if err := tx.root.spill(); err != nil {
tx.rollback()
return err
}
}
rebalance 函数
rebalance 做了如下操作:
- 如果当前节点没执行过
del方法(unbalanced为false),跳过当前节点。 - 如果当前节点的填充率大于25%且inode数量比最少数量大,则不处理该节点,以免
rebalance操作太频繁导致性能下降。 - 如果当前节点为根节点且只有一个孩子,那么将该根节点与唯一的孩子合并。需要注意的是,该孩子节点可能还有孩子,因此合并的时候需要修改相应的指针。合并后,释放孩子节点使用的page。
- 如果当前节点为空节点,删除当前节点并释放占用的page,并递归对父节点执行
rebalance操作。 - 否则,与兄弟节点合并。此时,如果当前节点在父节点中不是首个孩子,则默认与后继兄弟节点合并,否则与前驱兄弟节点合并。合并后,释放占用的page,并递归对父节点执行
rebalance操作。 - 由于此次调整可能会导致节点的删除,因此向上递归看是否需要进一步调整.
func (n *node) rebalance() {
if !n.unbalanced {
return
}
n.unbalanced = false
// Ignore if node is above threshold (25%) and has enough keys.
var threshold = n.bucket.tx.db.pageSize / 4
if n.size() > threshold && len(n.inodes) > n.minKeys() {
return
}
// Root node has special handling.
if n.parent == nil {
// If root node is a branch and only has one node then collapse it.
if !n.isLeaf && len(n.inodes) == 1 {
// Move root's child up.
child := n.bucket.node(n.inodes[0].pgid, n)
n.isLeaf = child.isLeaf
n.inodes = child.inodes[:]
n.children = child.children
// Reparent all child nodes being moved.
for _, inode := range n.inodes {
if child, ok := n.bucket.nodes[inode.pgid]; ok {
child.parent = n
}
}
// Remove old child.
child.parent = nil
delete(n.bucket.nodes, child.pgid)
child.free()
}
return
}
// If node has no keys then just remove it.
if n.numChildren() == 0 {
n.parent.del(n.key)
n.parent.removeChild(n)
delete(n.bucket.nodes, n.pgid)
n.free()
n.parent.rebalance()
return
}
// Destination node is right sibling if idx == 0, otherwise left sibling.
var target *node
var useNextSibling = (n.parent.childIndex(n) == 0)
if useNextSibling {
target = n.nextSibling()
} else {
target = n.prevSibling()
}
// If both this node and the target node are too small then merge them.
if useNextSibling {
// Reparent all child nodes being moved.
for _, inode := range target.inodes {
if child, ok := n.bucket.nodes[inode.pgid]; ok {
child.parent.removeChild(child)
child.parent = n
child.parent.children = append(child.parent.children, child)
}
}
// Copy over inodes from target and remove target.
n.inodes = append(n.inodes, target.inodes...)
n.parent.del(target.key)
n.parent.removeChild(target)
delete(n.bucket.nodes, target.pgid)
target.free()
} else {
// Reparent all child nodes being moved.
for _, inode := range n.inodes {
if child, ok := n.bucket.nodes[inode.pgid]; ok {
child.parent.removeChild(child)
child.parent = target
child.parent.children = append(child.parent.children, child)
}
}
// Copy over inodes to target and remove node.
target.inodes = append(target.inodes, n.inodes...)
n.parent.del(n.key)
n.parent.removeChild(n)
delete(n.bucket.nodes, n.pgid)
n.free()
}
// Either this node or the target node was deleted from
// the parent so rebalance it.
n.parent.rebalance()
}
函数的前半段都是对一些特殊情况做处理,从 useNextSibling开始才是它的正常逻辑,整个 过程叫 rebalance 其实并不准确,其实应该是 “合并”—— 把所有能合并的节点都合并了。
从最上面 事务 commit 调用 rebalance() 来看,rebalance 并不是从叶子结点开始的,实际上它是从 bucket.nodes 里面获取,而这是一个 map 结构,因此每次迭代都是无序的,所以每次 rebalance 的节点都是随机挑选。
func (b *Bucket) rebalance() {
// 对所有缓存的 node 进行调整
for _, n := range b.nodes {
n.rebalance()
}
// 对所有子 bucket 进行调整
for _, child := range b.buckets {
child.rebalance()
}
}
这样做不会出错的原因是: rebalance 本质就是在合并节点,只要一个节点size 小于 threshold,它就跟它的左(右)节点合并,因此顺序不重要。
spill 函数
与合并节点不同, spill 是递归到叶子结点再开始 spill 的。
具体过程如下:
- 判断
n.spilled标记,默认为 false,表明所有节点都需要调整。如果调整过,则跳过。 - 由于是自下而上调整,因此需要递归调用以先调整子节点,再调节本节点。
- 调整本节点时,将节点按照 pagesize 进行拆分。
- 为所有新节点申请新的合适尺寸的 pages,然后将 node 写入 page(此时还没有写回文件系统)。
- 如果 spilt 生成了新的根节点,则需要向上递归调用调整其他分支。为了避免重复调整,会将本节点
children置空。
func (n *node) spill() error {
var tx = n.bucket.tx
if n.spilled {
return nil
}
// Spill child nodes first. Child nodes can materialize sibling nodes in
// the case of split-merge so we cannot use a range loop. We have to check
// the children size on every loop iteration.
sort.Sort(n.children)
for i := 0; i < len(n.children); i++ {
if err := n.children[i].spill(); err != nil {
return err
}
}
// We no longer need the child list because it's only used for spill tracking.
n.children = nil
// Split nodes into appropriate sizes. The first node will always be n.
var nodes = n.split(uintptr(tx.db.pageSize))
for _, node := range nodes {
// Add node's page to the freelist if it's not new.
// 如果当前节点引用的page非空, 将释放当前占用的page,因为最后会写入到新的 page 中去。
// 另外,split出的新节点的页引用为空
if node.pgid > 0 {
tx.db.freelist.free(tx.meta.txid, tx.page(node.pgid))
node.pgid = 0
}
// Allocate contiguous space for the node.
p, err := tx.allocate((node.size() + tx.db.pageSize - 1) / tx.db.pageSize)
if err != nil {
return err
}
// Write the node.
node.pgid = p.id
node.write(p)
node.spilled = true
// Insert into parent inodes.
if node.parent != nil {
var key = node.key
if key == nil {
key = node.inodes[0].key
}
node.parent.put(key, node.inodes[0].key, nil, node.pgid, 0)
node.key = node.inodes[0].key
_assert(len(node.key) > 0, "spill: zero-length node key")
}
// Update the statistics.
tx.stats.Spill++
}
// If the root node split and created a new root then we need to spill that
// as well. We'll clear out the children to make sure it doesn't try to respill.
if n.parent != nil && n.parent.pgid == 0 {
n.children = nil
return n.parent.spill()
}
return nil
}
可以看出,boltdb 维持 B+ 树查找性质,并非像教科书 B+ 树一样,将所有分支节点的分支树维护在一个固定范围,而是直接按节点元素是否能够保存到一个 page 中来做的。这样做可以减少 page 内部碎片,实现也相对简单。
为什么要对 n.children 进行排序? children 是 []*node类型,Less 函数指定了比较大小的方式 Compare(s[i].inodes[0].key, s[j].inodes[0].key) 因此这里的 sort 就是让 B+树 分支节点保存的索引有序。
几个问题
- n.children 的作用看起来只是为了 spill 的时候用,用完就设置为 nil 了。为什么不需要保存全部的 children 信息呢? B+ 树节点不是应该保存所有的分支、叶子节点信息吗?
- n.children 是已实例化节点的node,那么在 合并和分裂的过程中,没有从 page 实例化成 node 的就不用管了? (在调用
nextSibling的过程中childAt就对节点 n 的左右兄弟就行了实例化,因此虽然说 children里不是全部 node,但是本次操作牵涉的所有 node 都会在其中 )